프언 ch3) 프로그래밍 언어의 구문 및 의미론
Syntax (구문) 과 Semantics (의미론)
1. Syntax (구문) - 프로그램에서 표현식, 문장, 프로그램 단위의 구조나 형식을 의미
2. Semantics (의미론) - 구문이 어떻게 의미를 가지는지, 즉 프로그램이 수행하는 동작을 정의
-> 구문과 의미론은 언어의 정의를 제공, 언어 사용자는 이를 통해 언어를 이해하고 활용
용어 정리 (Terminology)
1. 문장(sentence) - 언어에서 사용되는 문자열로, 알파벳 문자의 집합
2. 언어(Language) - 문장의 집합
3. 렉셈(Lexeme) - 언어에서 가장 낮은 수준의 구문 단위 (최소의 문법 단위)
ex) *, sum, begin
4. 토큰(Token) - 렉셈의 범주
ex) 식별자(identifier)와 같은 카테고리를 가짐
언어의 형식적 정의
1. 인식기 (Recognizers) - 언어의 알파벳을 기반으로 입력 문자열이 해당 언어에 속하는지 판단하는 장치
- 컴파일러의 구문 분석기(Syntax Analyzer) 가 이에 속함
2. 생성기 (Generators) - 문법 규칙을 사용하여 언어의 문장을 생성하는 장치
- 생성된 문장을 구문 분석기에서 비교하여 올바른지 확인할 수 있음
문맥-자유문법(Context-Free Grammer) 와 BNF
1. Context-Free Grammer(CFG)
- 언어의 구문을 정의하는데 사용
- Nonterminal 심볼, Terminal 심볼, 시작 심볼, 생성 규칙으로 구성
- Noam Chomsky에 의해 개발
Nonterminal 심볼 : 변환될 수 있는 심볼, 보통 대문자로 표시
Terminal 심볼 : 더 이상 변환되지 않는 기본 심볼, 보통 소문자로 표시
시작 심볼 S : Nonterminal 심볼 중 하나로 시작할 때 사용되는 심볼
생성 규칙 : 규칙을 통해 Nonterminal 심볼이 Terminal 심볼 또는 다른 Nonterminal으로 변환
2. Backus-Naur Form(BNF)
- 문법을 정의하기 위해 Nonterminal과 Terminal을 사용하여 구문 규칙을 작성하는 방식
- John Backus에 의해 개발
- context-free grammers와 동일하다
BNF 규칙
1. Nonterminal을 좌측에 두고, Terminal 및 다른 Nonterminal을 우측에 두는 형태로 정의
2. Nonterminal은 추상화된 표현, Terminal은 lexemes or tokens임
3. left-hand side(LHS)는 Nonterminal이고, right-hand side(RHS)는 Nonterminal이거나 Terminal임
4. Nonterminals은 종종 < > 안에 들어가 있음


Describing Lists
- Sytactic list(구문 리스트) 는 재귀를 사용하여 정의할 수 있음 (무한반복 가능)

유도 (Derivation)
- 유도는 시작 심볼에서부터 Terminal 심볼만(sentence) 남을 때까지 생성 규칙을 반복적으로 적용하는 과정
- sentential form 은 모든 문장, Terminal로만 이루어진 sentential form은 문장(sentence)임
- 좌측 유도(Leftmost Derivation) : 매 단계에서 가장 왼쪽의 Nonterminal을 확장하는 방법
- 우측 유도(Rightmost Derivation) : 매 단계에서 가장 오른쪽의 Nonterminal을 확장하는 방법

<program> =>* a = b + const로 요약해서 표현 가능

-> 생성할 스트링이 CFG 문법에 맞는지 확인 가능해야함!!!!!!!
만약 aa = bc + ab가 가능하도록 문법을 변경한다면!!!!!
(1)<var> -> a|b|c|d|<var><var>
----------------------------------------------------
(2)<var> -> <fact> | <var><fact>
<fact> -> a|b|c|d
Parse Tree (구문 트리)
- 구문 트리는 유도 과정을 트리 형태로 나타낸 것
- 트리의 루트는 시작 심볼이며, 각 노드는 생성 규칙을 적용하여 확장
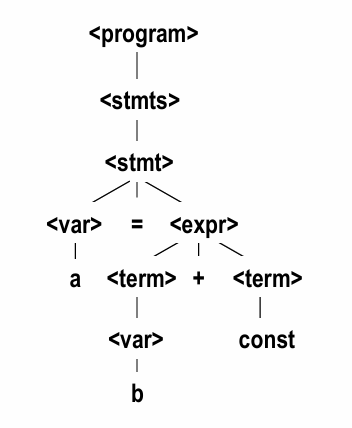
문법의 모호성 (Ambiguity in Grammars)
- 문법이 모호하다는 것은 동일한 문장을 두 개 이상의 Parse Tree로 표현할 수 있다는 것
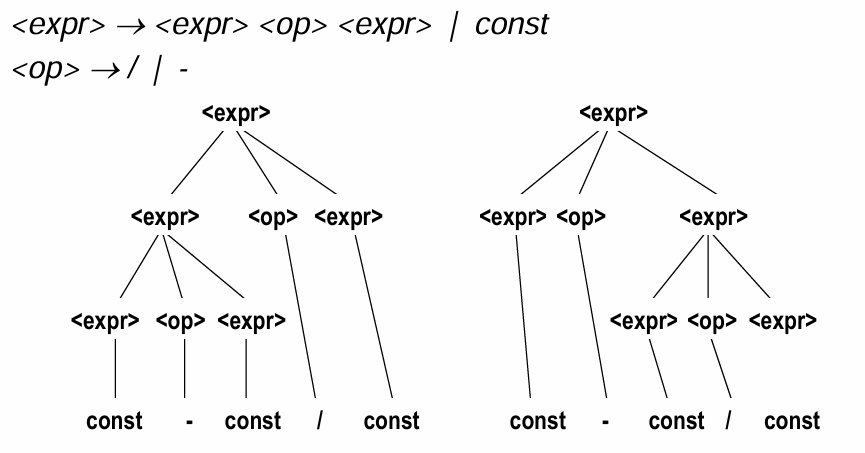
모호성하지 않은 표현
- <expr>와 <term>으로 각각 연산자 우선순위를 처리
- 우선순위가 높은 것은 나중에 적어줌
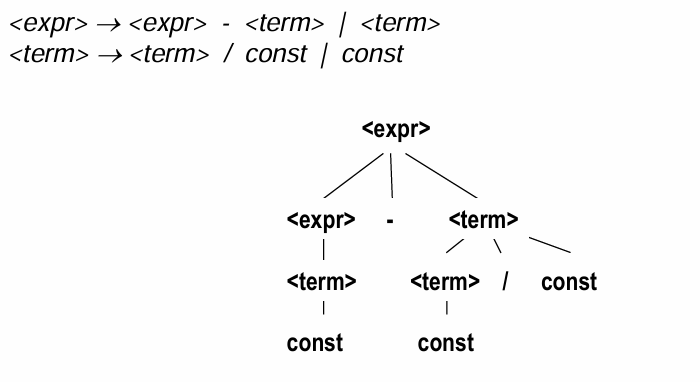
연산자의 결합법칙 (Associativity)
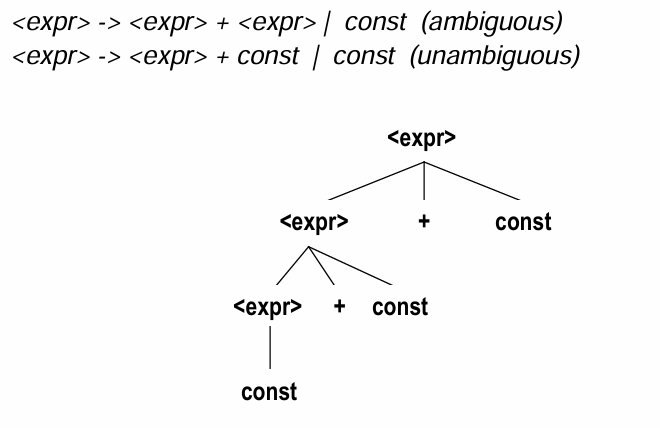
<expr> -> <expr> + const 는 Left Associativity를 가지고
<expr> -> const + <expr> 는 Right Associativity를 가짐
if-then-sle 문법의 모호성
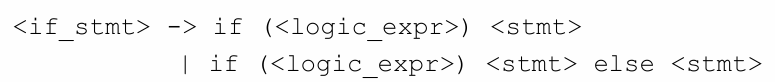
-> 모호성을 가지고 있음 (else가 포함된 문법에서는 어떤 if문에 해당하는 else가 매칭되는지 불명확할 수도 있음)

-> <matched>는 if문과 else가 제대로 매칭된 경우를 처리, <unmatched>는 아직 else가 매칭되지 않은 경우를 처리
확장된 BNF (Extended BNF)
-> BNF를 확장하여 옵션, 반복, 대체를 더 쉽게 표현함
1. Optional Parts (선택 사항)
- 선택적인 부분은 대괄호 [ ]로 표시 (해당 부분이 있어도 되고, 없어도 되는 경우
ex)
<proc_call> -> ident [ (<expr_list>) ]
<proc_call> -> ident | ident (<expr_list>)
2. Alernative Parts (대체)
- 우변(RHS)의 대체 가능한 부분은 괄호 ( ) 로 감싸고, 수직 막대 | 를 사용하여 구분 (여러 선택 가능한 표현식)
ex)
<term> -> <term> (+|-) <term>
3. Repetitions (반복)
- 반복은 중괄호 { }를 사용하여 나타냄 (해당 부분이 0회 이상 반복될 수 있음을 의미)
<ident> -> letter { letter | digit }
<ident> -> letter <ident2>
<ident2> -> letter | letter <ident2> | digit <ident2>

위의 예시에서 EBNF는 결합성이 없음
결합성이 있으려면
<expr> -> <expr> { (+ | -) <term> } | <term>
<term> -> <term> { (* | /) <factor> } | <factor>
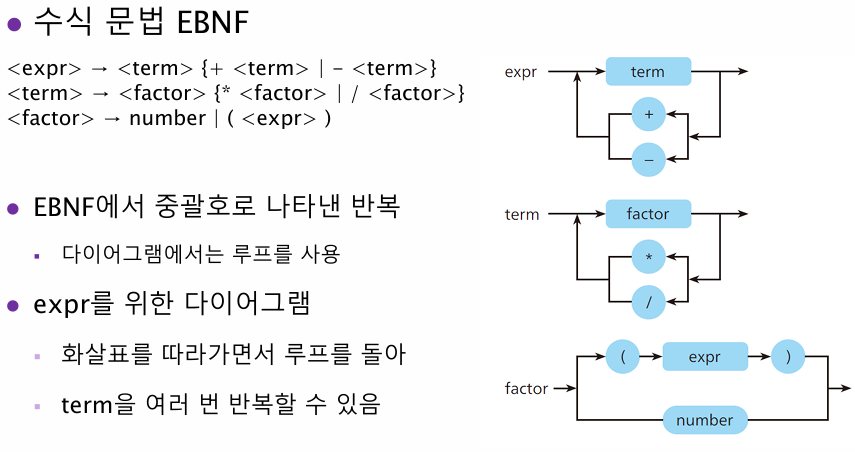
구문 다이어그램

Static Semantics (정적 의미론)
1. 정적 의미론은 프로그램의 구조적 규칙에 대해 다루며, 프로그램의 의미와는 직접적인 관련 없음
2. Context-free grammers(CFG)는 프로그래밍 언어의 모든 문법을 설명할 수 없음
3. CFG의 제약 (연산자의 피연산자 타입은 처리 어려움)
CFG가 아닌 부분의 제약 (변수는 사용되기 전에 선언되어야 한다는 규칙은 표현할 수 없음)
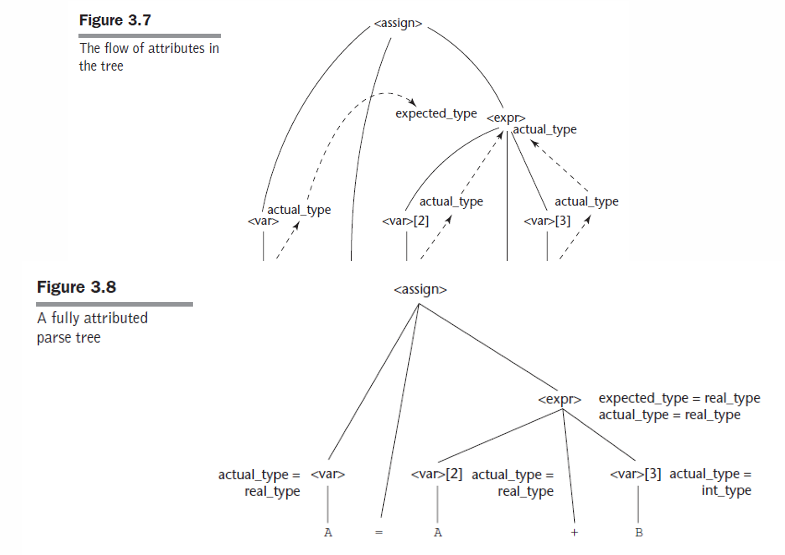
Attribute Grammars -> static semantics
- 속성 문법 (AGs) 은 CFG를 확장하여 구문 트리의 각 노드에 의미적 정보를 추가하는 방법
- 이를 통해 정적 의미론을 표현하고, 프로그램의 정확성을 체크
1. 합성된 속성 (Synthesized Attributes)
- 트리의 자식에서 값을 계산하여 부모로 전달하는 방식
2. 상속된 속성 (Inherited Attributes)
- 부모에서 자식으로 값을 전달하는 방식

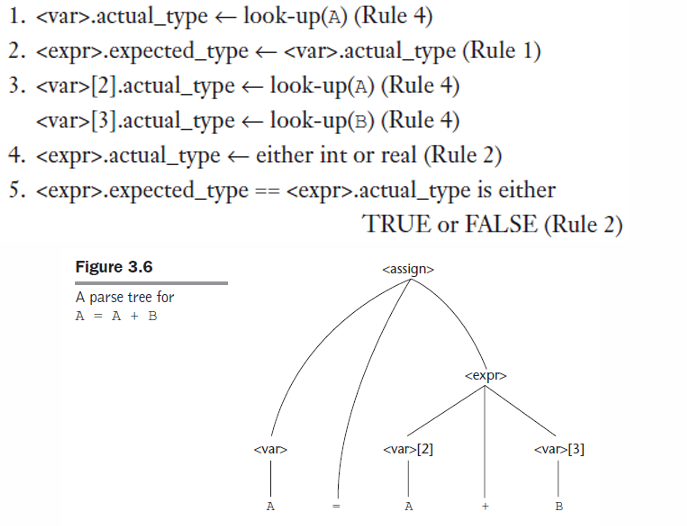
1. 예시
Syntax rule : <expr> -> <var>[1] + <var>[2]
Sematic rules : <expr>.actual_type <- <var>[1].actual_type
Predicate(명제) - 참/거짓 :
<var>[1].actual_type == <var>[2].actual_type
<expr>.expected_type == <expr>.actual_type
2. 예시
Syntax rule : <var> -> id
Sematic rules : <var>.actual_type <- lookup(<var>.string)
Attribute values 계산 방법
1. 모든 속성이 상속된 경우
- 트리는 상향식(top-down)으로 장식. 즉, 부모 노드에서 자식 노드로 속성 값이 전달
- 각 부모 노드는 자식 노드로 값을 전달하면서 트리의 상단에서 하단으로 계산이 진행
2. 모든 속성이 합성된 경우
- 트리는 하향식(bottom-up)으로 장식. 즉, 자식 노드에서 부모 노드로 속성 값이 계산
- 자식 노드부터 부모 노드로 올라가며 값을 계산하여 트리의 하단에서 상단으로 속성 값이 전달
3. 상속 속성과 합성 속성이 혼합된 경우
- 예를 들어, 부모에서 자식으로 전달되는 속성 값이 있고, 자식에서 부모로 계산되는 속성 값도 있음.

Semantics (의미론)
- 의미론을 정의하는 데에는 하나의 방법만 있는 것은 아님
- 주로 운영 의미론(Operational Semantics), 기호적 의미론(Denotational Semantics), 공리적 의미론(Axiomatic Semantics)
1. 운영 의미론(Operational Semantics)
- 프로그램의 동작을 기계 연산으로 설명하는 방법임.
- 상태 변화를 통해 그로그램이 수행하는 동작을 모델링함
- 형식적인 운영 의미론은 복잡하지만, 언어 학습이나 특징 설명에 유용
- 구현해서 보여주는 것이 더 좋지만 구현이 어려움
2. 기호적 의미론(Denotational Semantics)
- 수학적 객체를 사용하여 언어 구성 요소의 의미를 정의하는 방식
- 각 언어 요소는 수학적 객체로 매핑
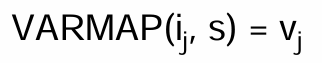
----------------------------------------------
S1 = { (x, 10), (y, 100), (z, 30) }
x = y+z
S2 = { (x, 130), (y, 100), (z, 30) }
----------------------------------------------
VARMAP(y, S1) = 100
VARMAP(z, S2) = 30

M(326) = M(32) * 10 + 6
= (M(3) * 10 + 2) * 10 + 6
