통계적 학습의 예시 : 광고 데이터 (Advertising data)
- 목표 : want to improve sales of your shoes (control advertising budgets : SNS, streaming, and filter)
How ?
1) learn the relationship between advertising and sales
2) use it to predict sales

핵심 용어 (Key terms)

1. want to improve sales(Y) of a product
-> Y : output variable, dependent variable
2. control advertising budgets : SNS(X1), streaming(X2), filter(X3)
-> X1, X2, X3 : input variable, independent variables, predictors
Key questions
1. What is the relationship between X1, X2, X3 and Y? -> learning
2. How accurately can we predict Y from X1, X2, X3? -> prediction
Formally,

- statistical learning : estimate (learn) f from data !
(There are many ways! You should be able to choose the best one!)
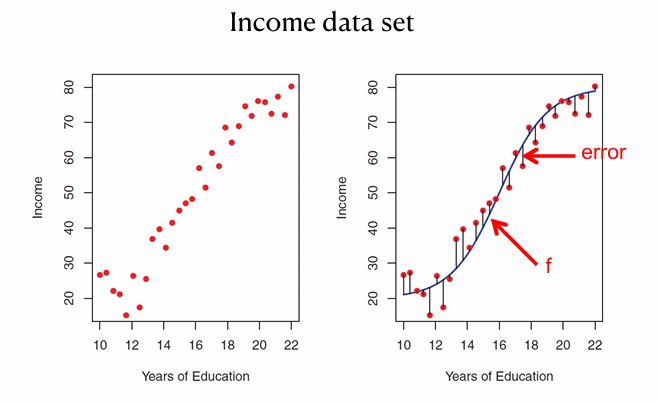
Why estimate f ?
모델의 유용한 용도
1) prediction : predict Y from (new or unseen) X
2) inference : understand the relationship between X and Y
Prediction
Once we have a good model, we can predict Y from new X

Reducible vs irreducible errors
- True relationship : Y = f(X) + e
- learn f from data and use it for prediction


1. 축소 가능한 오류 (Reducible error)
- 추청 함수 f^ 와 실제 함수 f 간에 차이가 있을 때 발생하는 오류
- f^ -> f 로 개선 가능하기 때문에 줄일 수 있는 오류
2. 축소 불가능한 오류 (Irreducible error)
- 데이터 자체의 불확실성이나 잡음으로 인해 발생하며, 모델이 아무리 개선되더라도 완전히 해결될 수 없음

Quantification of the error

-> reducible error를 최소화하기 위해 f 를 추정하는 것이 목표
---------------------------------------------------------------------------------------------------------------
Inference
- In prediction, f는 block box 였음
- But, for inference, 우리는 f의 정확한 형태를 알기를 원함
- X1, ..., Xp에 의해 Y가 어떻게 변하는지를 이해해야함! (X와 Y 관계를 찾기)

Inference Questions
1. Which predictors are associated with the response ?
-> 어떤 예측 변수가 반응변수(Y)와 관련이 있는가?
ex) X1, ...., Xp 중 어떤 변수가 중요한가?
2. What is the relationship between the response and each predictor ?
-> 반응변수와 예측변수 간의 관계는 무엇인가?
ex) X1이 증가하면 Y는 증가하는가? 감소하는가?
X2가 양수일 때, X1이 증가하면 Y는 증가하는가? 감소하는가?
3. Can the relationship between Y and each predictor be adequately summarized using a linear equation, or is the relationship more complicated ?
-> Y와 예측변수 간의 관계를 선형 방정식으로 유약할 수 있는가? 아니면 더 복잡한가?
------------------------------------------------------------------------------------------------------------------------------------------------------
Prediction vs Inference

문제 상황 :
- 90,000명의 사람들이 있고, 각각에 대해 400개의 특성(변수)이 있음
- 각 개인이 얼마를 기부할지를 예측하고 싶음
X1, ..., Xp : 인구통계학 데이터
Y : 긍정/부정 응답
핵심 질문 :
- 특정 개인에게 마케팅 메일을 보내야 할까?
=> 즉, Y값(기부 금액 또는 반응 유무)을 어떻게 추정하느냐는 중요하지 않음
(Don't care how you estimate Y) - 결과 예측만 중요!

목표 : 어떤 광고 매체가 매출에 영향을 미치는지 이해하는 것
질문들 :
- 어떤 매체가 매출에 기여하는가?
- 어떤 매체가 가장 큰 매출 상승을 유도하는가?
- SNS 광고가 늘어났을 때, 매출은 얼마나 증가하는가?
=> 광고의 인과적 효과를 이해하고자 하는 것이 핵심 (단순 예측이 아니라 이해와 설명이 목적)

목표 : 14개의 변수로 주택 가격을 예측하면서, 어떤 요인이 가격에 가장 큰 영향을 주는지 이해
핵심 :
- 단순히 예측하는 것이 아니라, 어떤 요인이 가격에 영향을 주는지 파악하고,
- 그 영향이 얼마나 큰지(효과 크기) 알고자 함
ex) 좋은 뷰 -> 집값 상승
How do we estimate f ?
- training data {(x1, y1), (x2, y2), ... , (xn, yn)}에서 우리는 estimate f하기를 원한다.
- 2개의 접근 타입
- parametric methods
- non-parametric methods

Parametric methods
모델의 파라미트의 수가 정해져 있음
Step 1. 모델 가정 (Assumption a model)
- 함수의 형태를 먼저 가정
- ex) 선형 모델(linear model) 가정
Step 2. 모델 적합(fit the model)
- 학습 데이터를 사용하여 가정한 모델의 파라미터 β0,β1,...,βp 를 추정
- 일반적으로 최소제곱법(least squares) 사용
=> 선형 모델은 단지 p+1개의 계수만 추정하면 됨!

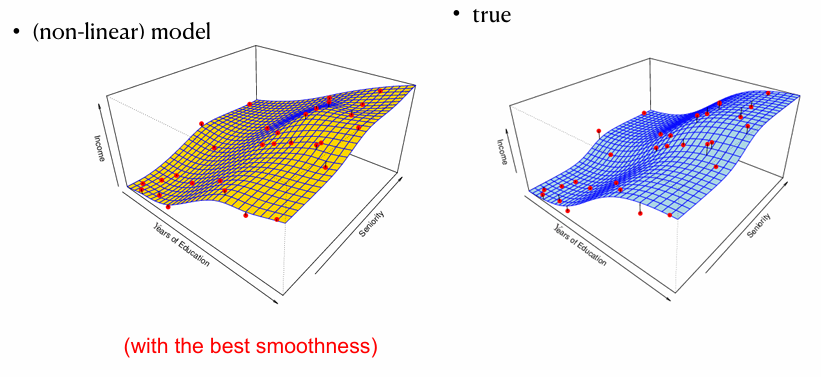
Non-parametric methods
모델의 파라미트의 수가 정해져 있지 않음
- 모델 형태에 대한 가정을 하지 않음
- 함수 f의 정해진 수학적 형태를 미리 가정하지 않음
- 데이터가 말해주는 대로 유연하게 모델링
- 장점 : 유연성(flexibility)가 높음, 훨씬 더 다양한 형태의 함수 f를 적합할 수 있음 (예: 비선형, 꺾인 함수 등)
- 단점 : 학습이 어렵고 복잡, 많은 양의 데이터가 필요함
-----------------------------------------------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------------------------------------------

Flexibility vs interpretability
- Simple models are easier to interpret!
ex) linear regression


'머신러닝' 카테고리의 다른 글
| 머신 러닝 ch5) Multiple Linear Regression (0) | 2025.03.26 |
|---|---|
| 머신 러닝 ch4) Simple Linear Regression (1) | 2025.03.26 |
| 머신 러닝 ch3) 모델 정확도 평가 (Assessing Model Accuracy) (1) | 2025.03.25 |
| 머신 러닝 ch1) 통계적 학습 개요 (2) | 2025.03.25 |