문해 ch2) Feasibility of Learning (학습의 실현 가능성)

Learning the target function

- target function f = 학습 목표

  -> f에 대한 중요한 정보는 알려지지 않음

 

- 자연스러운 질문

  -> 어떻게 제한된 data set이 entire f를 결정하는데 충분한 정보를 보여줄까?

 

 

Inference outside training data (훈련 데이터 외부의 추론)

 - 훈련 데이터(training data)를 넘어서 보지 않은 데이터(test) 에 대해 추론하는 능력 = 일반화 (generalization)

 

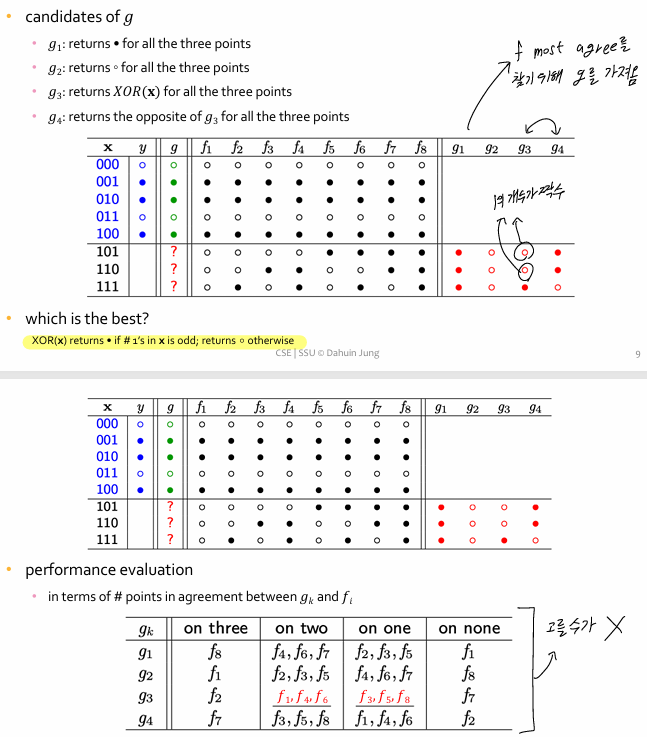
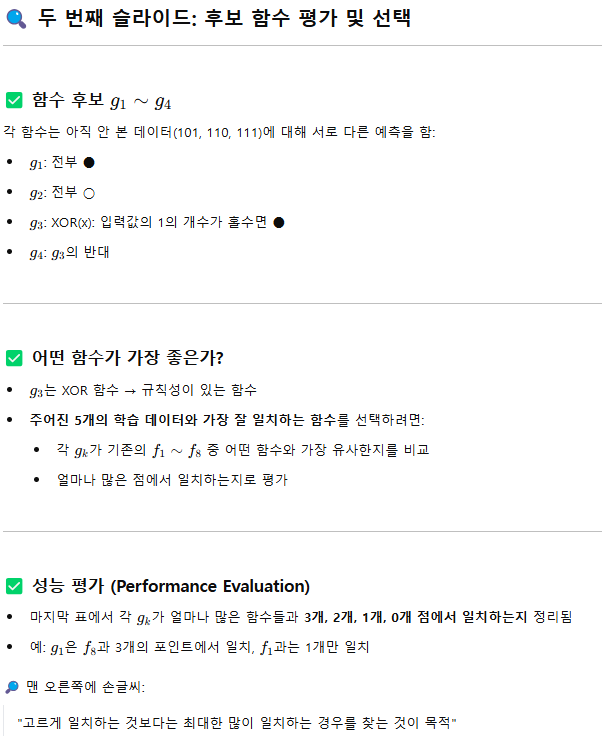
1. In training data D, we know the value of f on all points

  - 훈련 데이터에서는 f(x)의 값을 다 알고 있음

  - 하지만 이건 우리가 진짜 f라는 함수를 완전히 배웠다는 의미는 아님

  - 그냥 암기만 했을 수도 있음

 

2. Key question : does D tell us anything outside D?

 - 핵심 질문 : 훈련 데이터 외부의 데이터에 대해 뭔가 알려줄 수 있는가?

 

 - 알려줄 수 있다면 -> 진짜 뭔가를 배운 것

 - 그렇지 않다면 -> 학습이 불가능하거나 의미 없음

 

문제 상황

 

 

------------------------------------------------------------------------------------------------------------------------------

 

문제 풀이

---------------------------------------------------------------------------------------------------------------------------

Hoeffding Inequality (수학적 불평등)

Rescue Plan : 학습을 "확률적 추론" 으로 구제

- 학습이 어려운 이유는 : 우리는 훈련 데이터 D만 알고, 전체 함수 f를 모름

- 그래서 전략을 바꿈 -> 정확하게 f를 알 수는 없지만, 높은 확률로 f에 근접한 것을 추정할 수 있으면 학습은 가능(feasible)

 

=> 결정론적 추정 대신, 확률적 추정으로 학습 가능성을 열어줌

 

 

A 'Bin' Experiment (구슬통 실험)

설정 : 

1. 구슬통(bin)에 빨간색/초록색 구슬이 무한히 많이 있음

2. 빨간 구슬일 확률 : μ

3. 초록 구슬일 확률 : 1 - μ

 -> 우리는 실제로 이 확률 μ를 모름

 

실험 :

1. 이 통에서 구슬 N개를 복원 추출(with replacement) 하여 관측

2. 샘플 안에서 빨간 구슬 비율 :  μ^​

-> 목표 : μ^를 통해 진짜  μ를 추정할 수 있을까?

 

μ^를 통해 진짜  μ를 추정할 수 있을까?

 

답 : 항상은 아니다 (샘플이 빨간색 위주로 나올 수도 있고, 초록색 위주로 나올 수도 있음)

      그러나 확률적으로 보자면 샘플 수 N이 충분히 크면 μ^는 μ에 가까워질 가능성이 매우 높음

=> 이 사실을 수학적으로 정량화해 주는 게 바로 Hoeffding Inequality!!

 

Hoeffding Inequality

 

수식

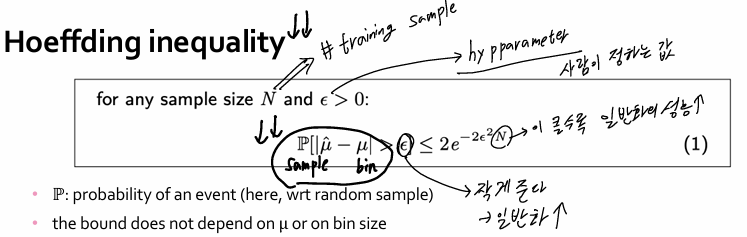
해석:

• ϵ: 우리가 허용 가능한 오차
• N: 샘플 수
• 위 확률은:
  → "샘플 평균이 진짜 평균보다 ϵ 이상 차이날 확률"은
  → N이 커질수록 빠르게 0에 수렴

🧠 핵심 아이디어:

• 적은 수의 표본으로는 불확실하지만,
• 많은 표본이 있을수록 우리가 모르는 진실(μ)에 점점 가까워질 수 있다!

 

Connection to Learning

- 구슬 문제에서는 단 하나의 숫자(확률)를 추정함

- 학습에서는 전체 함수를 추정해야 하니 훨씬 복잡함

=> but! 우리는 이 둘을 연결해서 분석 가능

 

 

Bin coloring ≡ Hypothesis h

- 하나의 가설 h∈H를 선택하면, 입력 x에 대해 h(x) 값을 줄 수 있음

 

-> h가 f에 가까울수록, 구슬통 전체의 빨간색 비율(오류율 μ)은 작아짐

   그런데 전체를 못 보니까 샘플에서의 빨간색 비율(μ^)만 관측됨

   Hoeffding 부등식을 통해 -> 샘플에서 작은 오류율이 전체에서도 작을 가능성이 높다고 판단

 

=> 학습 알고리즘은 다양한 가설 h 중에서 오류율이 낮은 h를 찾으려고 하는 것

------------------------------------------------------------------------------------------------------------------------------------

 

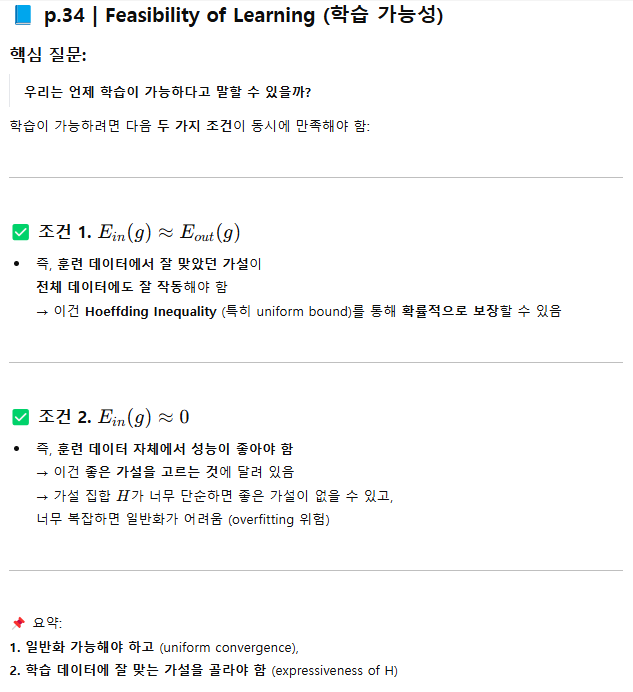
Are we done?

위의 예시는 한 가설에 대해 Hoeffding 부등식을 적용 but 현실에서는 ?

- 실제 머신러닝에서는 하나의 h를 평가하는 게 아님

- 우리는 수많은 가설 h1, h2, ..., hM ∈ H 중에서 하나를 선택해야 함

 

=> 즉, 우리가 관찰한 Ein​(h)이 진짜 오류 Eout(h)를 대표하려면, 모든 가설 h∈H에 대해 동시에 적용 가능해야 함